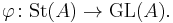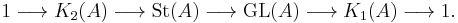Steinberg group (K-theory)
In algebraic K-theory, a field of mathematics, the Steinberg group 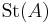 of a ring A, is the universal central extension of the commutator subgroup of the stable general linear group.
of a ring A, is the universal central extension of the commutator subgroup of the stable general linear group.
It is named after Robert Steinberg, and is connected with lower K-groups, notably 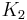 and
and 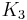 .
.
Contents |
Definition
Abstractly, given a ring A, the Steinberg group 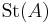 is the universal central extension of the commutator subgroup of the stable general linear group (the commutator subgroup is perfect, hence has a universal central extension).
is the universal central extension of the commutator subgroup of the stable general linear group (the commutator subgroup is perfect, hence has a universal central extension).
Concretely, it can also be described by generators and relations.
Steinberg relations
Elementary matrices—meaning matrices of the form 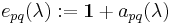 , where
, where 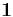 is the identity matrix,
is the identity matrix, 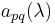 is the matrix with
is the matrix with  in the
in the 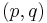 entry and zeros elsewhere, and
entry and zeros elsewhere, and 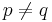 —satisfy the following relations, called the Steinberg relations:
—satisfy the following relations, called the Steinberg relations:
The unstable Steinberg group of order r over A, 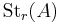 , is defined by the generators
, is defined by the generators 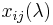 ,
, 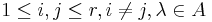 , subject to the Steinberg relations. The stable Steinberg group,
, subject to the Steinberg relations. The stable Steinberg group, 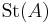 , is the direct limit of the system
, is the direct limit of the system 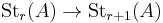 . It can also be thought of as the Steinberg group of infinite order.
. It can also be thought of as the Steinberg group of infinite order.
Mapping 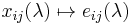 yields a group homomorphism
yields a group homomorphism
As the elementary matrices generate the commutator subgroup, this map is onto the commutator subgroup.
Relation to K-theory
K1
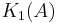 is the cokernel of the map
is the cokernel of the map 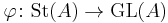 , as
, as 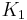 is the abelianization of
is the abelianization of 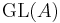 and
and  is onto the commutator subgroup.
is onto the commutator subgroup.
K2
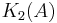 is the center of the Steinberg group; this was Milnor's definition, and also follows from more general definitions of higher K-groups.
is the center of the Steinberg group; this was Milnor's definition, and also follows from more general definitions of higher K-groups.
It is also the kernel of the map 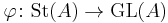 , and indeed there is an exact sequence
, and indeed there is an exact sequence
Equivalently, it is the Schur multiplier of the group of elementary matrices, and thus is also a homology group: 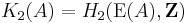 .
.
K3
Gersten (1973) showed that 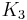 of a ring is
of a ring is 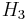 of the Steinberg group.
of the Steinberg group.
References
- Gersten, S. M. (1973), "
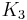 of a Ring is
of a Ring is 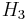 of the Steinberg Group", Proceedings of the American Mathematical Society (American Mathematical Society) 37 (2): 366–368, doi:10.2307/2039440, JSTOR 2039440
of the Steinberg Group", Proceedings of the American Mathematical Society (American Mathematical Society) 37 (2): 366–368, doi:10.2307/2039440, JSTOR 2039440 - Milnor, John Willard (1971), Introduction to algebraic K-theory, Annals of Mathematics Studies, 72, Princeton University Press, MR0349811
- Steinberg, Robert (1968), Lectures on Chevalley groups, Yale University, New Haven, Conn., MR0466335, http://www.math.ucla.edu/~rst/
![\begin{align}
e_{ij}(\lambda) e_{ij}(\mu) &= e_{ij}(\lambda%2B\mu) \\
\left[ e_{ij}(\lambda),e_{jk}(\mu) \right] &= e_{ik}(\lambda \mu) && \mbox{for } i \neq k\\
\left[ e_{ij}(\lambda),e_{kl}(\mu) \right] &= \mathbf{1} && \mbox{for } i \neq l, j \neq k\\
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/6408aaa77c355c0dc7bfab3fe837d16f.png)